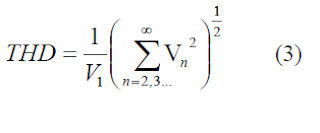1. INTRODUÇÃO
Com o avanço tecnológico, uma gama cada vez maior de aparelhos mais compactos e com componentes variados é lançada no mercado. Com isso, problemas que antes eram desconhecidos apareceram, como exemplo, podemos citar harmônicos de corrente que foram notadas após a implementação de componentes não-lineares nos circuitos dos equipamentos e a interferência eletromagnética proveniente da redução das dimensões das placas de circuito impresso e aproximação dos dispositivos. Nos USA, estima-se que num período de 10 anos as cargas eletrônicas foram duplicadas, com uma previsão de atingir 90% no ano de 2010[1].
Este trabalho está relacionado ao estudo de componentes harmônicas que surgem nas ondas de senoidais de corrente.
2. HARMÔNICOS
Os harmônicos de corrente surgem devido à presença de cargas não-lineares na rede de distribuição. Essas cargas não possuem uma relação linear entre tensão e a corrente como cargas resistivas, capacitivas e indutivas. Estas podem ser geradas por equipamentos elétricos e eletrônicos que possuem componentes não-lineares tais como: diodos, transistores, chaves manuais entre outros.
As cargas não-lineares absorvem uma corrente diferente da forma de onda da tensão que a alimenta, gerando uma perturbação na onda da corrente.
A harmônica é uma componente adicional que possui freqüência múltipla da onda senoidal fundamental. Na figura 1 está ilustrada, a componente fundamental da tensão e sua quinta harmônica. Na figura 2 é apresentada a forma de onda da tensão resultante, que neste caso é a soma das duas componentes apresentadas na figura1.
As harmônicas que causam maior distorção na onda da corrente são geralmente as de ordem ímpar e quanto menor sua freqüência, maior será distorção.
A distorção harmônica das tensões nos pontos de conexões depende fundamentalmente das harmônicas de corrente injetada ou drenada e da impedância da rede neste ponto.
Figura 1: Onda fundamental com sua harmônica n=5 abaixo
Figura 2: Onda resultante da soma da onda da tensão e da harmônica n=5
3. COMO DETECTAR AS HARMÔNICAS?
Há vários métodos que permitem analisar e quantificar as distorções na forma das ondas. Podem-se destacar quatro deles que serão apresentados a seguir:
3.1 Fator de Potência
O fator de potência é a relação entre a potência ativa (P) e a aparente (S), que possuem uma relação:
FP = | Potência Ativa (P) |
Potencia Aparente (S) |
Atualmente as normas técnicas brasileiras regulamentam o fator de potência mínimo de uma instalação elétrica em 92% e em algumas classes de equipamentos este limite chega a 97% [2].
As perdas de transmissão de energia elétrica são proporcionais ao quadrado da corrente eficaz que circula pelos condutores. Assim, para uma dada potência ativa, quanto menor for o FP, maior será a potência reativa e, conseqüentemente, a corrente pelos condutores. A figura 4 mostra o aumento das perdas em função da redução do FP [3].
Figura 4 - O gráfico mostra a relação entre as perdas e o fator de potência. Pode-se observar que quanto maior o FP menor a perda de energia.
3.2 Fator Crista
O fator crista é encontrado através da razão entre o valor da corrente I
O fator de crista típico das correntes absorvidas pelas cargas não-lineares pode tomar valores entre 1,5 a 2, chegando até 5 nos casos críticos.A distorção harmônica é a medida da perturbação do sinal na saída, após este passar por todo equipamento, em relação ao sinal aplicado na entrada do aparelho. A distorção do sinal é gerada pelo acréscimo de freqüências múltiplas do sinal fundamental que surgem devido a não-linearidade de alguns componentes presentes no circuito.
O THD é definido como: Onde V1 é a tensão fundamental e Vn é a tensão harmônica de ordem n.
3.3 Distorção Harmônica Total (THD)
A distorção harmônica é a medida da perturbação do sinal na saída, após este passar por todo equipamento, em relação ao sinal aplicado na entrada do aparelho. A distorção do sinal é gerada pelo acréscimo de freqüências múltiplas do sinal fundamental que surgem devido a não-linearidade de alguns componentes presentes no circuito.
O THD é definido como:
3.4 Fator de Distorção (DF)
O fator de distorção indica que a quantidade de distorção harmônica que remanesce em uma forma de onda particular após suas harmônicas ser sujeitas a uma atenuação de segunda ordem (filtro LC).
Assim, o DF é uma medida eficaz que reduz harmônicas não desejadas, sem ter que especificar os valores de um filtro da carga de segunda ordem [5]. Podemos encontrar o DF através da fórmula:
4. IMPACTOS ECONÔMICOS
A corrente harmônica acarreta perdas suplementares de energia, causando desde danos aos componentes até a parada do equipamento. A seguir estão algumas conseqüências da circulação dessas distorções por equipamentos e na rede.
- Sobrecarga e envelhecimento precoce do equipamento, levando este a ser substituído.
-O aumento do pico da corrente causa disparos intempestivos, podendo causar falha de operação do material.
-Possíveis medições errôneas, gerando um aumento na conta.
-Interferências no sistema de telecomunicação (ruídos).
-Sobreaquecimento das máquinas.
5. NORMAS PARA EMISSÃO DE HARMÔNICAS NA REDE
As correntes distorcidas podem afetar na operação de outros equipamentos também ligados à rede elétrica, e causar outros problemas que afetam a qualidade da energia elétrica fornecida aos consumidores. Dessa forma, o sistema elétrico como um todo, fica prejudicado devido à soma de milhões de equipamentos “poluindo” a rede pública [4].
Para controlar essas correntes, foram estabelecidas normas limitando a emissão de harmônicas por equipamentos elétricos e eletrônicos encontrados em todos os setores.
Há várias normas que englobam harmônicas, visando diminuir sua expansão. Pode-se citar como exemplo a norma IEC 6100-3-2 que limita a emissão de harmônicas por equipamentos elétricos e eletrônicos com corrente de entrada menor que 16A por fase.
As harmônicas geradas por um aparelho não podem ultrapassar os níveis especificados e devem funcionar normalmente na presença das perturbações iguais aos níveis especificados.
Juliana Avena Maia & José Renes Pinheiro
Curso de Engenharia Elétrica – UFSM –Santa Maria-RS